
こんにちは。プロダクトマネージャーの tora です。
この記事は「SmartHRのプロダクトマネージャー全員でブログ書く2024」への参加記事です。
25人が持ち回りで毎週記事を投稿します。ぜひご覧ください!
私が所属しているチームで1ヶ月ほど前に 申請にて代理提出できる機能 をリリースすることができ、その開発プロセスをチームで振り返っている際、ある仮説が立ちました。
その仮説を検証するにあたって「推測統計学」が活かせそうだったので、今回はその話を書きたいと思います。
仮説
申請機能のユーザーは、設定例を見ていると活用しやすいのではないか。
SmartHRでは機能提供する際、合わせてヘルプページを作成しており、ヘルプページは大きく分けて6種類存在します。その1種である「設定例」を閲覧しているユーザーは、申請機能の活用度合いが高いかもしれないという仮説です。
この仮説が立った背景として、申請機能における各ヘルプページのページビュー数を確認していた際、「設定例」のページビュー数が他種類と比較して多く、もしかすると機能の活用度合いに何か関係あるのでは?と気になりました。
検証内容
「設定例」の閲覧の有無が機能の活用度合いに影響を与えるのか、その影響度は偶然の範囲なのか否か、を検証します。
検証における前提
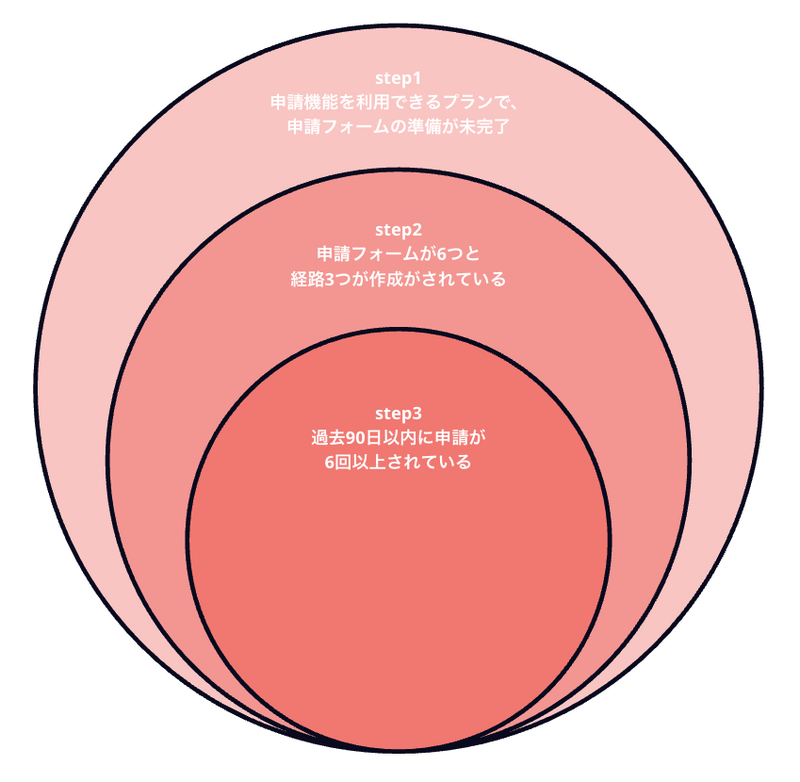
まず、申請機能の活用度合いを以下3ステップに分類します。
※経路と申請フォーム数はテスト的な利用をある程度除外するために下限を設けています
次に、特定ヘルプページの閲覧状況を以下2つに分類します。
- 設定例の閲覧あり
- 設定例の閲覧なし
最後に、各企業様を従業員規模に応じて、5つのグループに分類し、各グループ毎に設定例の閲覧有無が、活用度合いに影響を与えるのかを確認しました。
検証結果
いきなり、結果発表ですが、5つのグループのうち、4グループは観測されたデータが期待された分布と有意に異なることを示すことができました。
よって、機能概要や操作方法だけではなく、より具体的な使い方に踏み込んだヘルプページが活用度合いに影響を及ぼすということが統計的にわかりました。
検証結果を通して今後、新規機能を提供する際には「設定例」ページをどのように作るべきか、これまで以上にチームと深く議論することに繋がりそうです。
※以下にて、どのような検証を経て結果を導いたのか見ていきます
検証方法
今回の検証は「申請機能の活用度合い3ステップ」と「設定例の閲覧有無」という質的データ同士の検証となるため、カイ二乗検定を採用することにしました。 ※ここから少し統計の話が続きます
カイ二乗検定の流れは以下となります。
- 観測値と期待値がマッピングされた集計表を作成します。
- 今回は、3x2の集計表をグループ毎に作成します。
- 帰無仮説と対立仮説を設定します。
- 帰無仮説:活用例の閲覧有無が申請機能の活用度合いに影響を及ぼさない
- 対立仮説:活用例の閲覧有無が申請機能の活用度合いに影響を及ぼす
- 自由度を確認します。
- 今回集計表が3x2のため、自由度は2となります。
- 自由度2における上側確率を有意水準(p値) を0.05(=5%)と比較し検定します。
- 算出されたp値 > 0.05:帰無仮説を採択する(申請機能の活用度合いに設定例の閲覧有無は関係ない)
- 算出されたp値 < 0.05:帰無仮説を棄却する(申請機能の活用度合いに設定例の閲覧有無は関係ある)
※ただし、帰無仮説が棄却されないということは、帰無仮説が正しいということではなく、単に検定により得られた結果が帰無仮説と矛盾しないことがわかったということがわかっただけ、という点が注意です。
データ
5つのグループ毎に「観測値」と「期待値」を用意します。
今回p値が極端に小さくなることを避けるため、母集団から観測比率を算出、適切なサンプルサイズと観測比率をかけ算することで観測値を決めようとしました。その際、気になるのが「サンプル数ってどれくらいが適切なの?」です。
統計的検定でサンプル数を求めるには、以下4つのうちの3要素が決まれば残り1つが決まるとされています。

今回のケースを上記に当てはめてサンプル数を計算すると「62」となったので、切りよく60として、各グループ毎の「観測値」「期待値」表を作成します。
※最近はサンプル数を算出するためのソフトなどもあるので、うまく活用してみてください
観測値
| 設定例の閲覧あり | 設定例の閲覧なし | 合計 | |
|---|---|---|---|
| ステップ1 | ① | ② | ①+②=20 |
| ステップ2 | ③ | ④ | ③+④=20 |
| ステップ3 | ⑤ | ⑥ | ⑤+⑥=20 |
| 合計 | ①+③+⑤ | ②+④+⑥ | ①~⑥=60 |
期待値
| 設定例の閲覧あり | 設定例の閲覧なし | 合計 | |
|---|---|---|---|
| ステップ1 | n1*m1/N | n1*m2/N | n1=20 |
| ステップ2 | n2*m1/N | n2*m2/N | n2=20 |
| ステップ3 | n3*m1/N | n3*m2/N | n3=20 |
| 合計 | m1 | m2 | N=60 |
検定
上記観測値は非公開になりますが、①〜⑥に観測値を当てはめ、期待値が計算され、p値を算出すると以下の結果となりました。
- グループ1:0.0000
- グループ2:0.0059
- グループ3:0.0173
- グループ4:0.0445
- グループ5:0.1085
上記の結果、グループ1〜4までは帰無仮説を棄却し(=対立仮説を採択する)、グループ5は帰無仮説を採択する結果となりました。
最後に
ここまで読んでいただきありがとうございました。
今回は推測統計学を用いてデータ分析を行ってみましたが、改めて感じたことは、基本的なことですが「問い・仮説を立てること」です。そこがないとどんなデータが必要で、どのような分析手法が最適で、どのように検証するのか?が定まりません。
また、問い・仮説がないままデータ分析を行った結果は大抵の場合「せやんな〜」で終わってしまい、そこから得られたことを糧にネクストアクションや新しい仮説へと繋がっていきません。
今回のデータ分析・結果を通して、提供している「SmartHR スクール」の利用状況も機能の活用度合いに影響を与えるのでは?という新しい仮説が見えたので、またデータ分析から検証を行うことが楽しみです。
私たちはプロダクトマネージャーを募集しています!
SmartHRでは引き続きPMの採用に注力しています。
PM職に関する情報をまとめた記事がありますので、ぜひご一読ください。カジュアル面談のリンクなどもこちらに掲載しております。
SmartHRのプロダクトマネージャー職にご興味をお持ちの方へ